VC Copilotの使い方
VC Copilotとは
VC CopilotはDiscordサーバー上に簡単に導入できる通話データの収集/可視化を行うDiscord Botです
ここでは、VC Copilotの機能と用意されているコマンドについて説明します
通話の通知メッセージ
通話が開始/終了した時にテキストチャンネルに通知メッセージが送信されます
終了時のメッセージでは、その通話に参加したユーザー全員の参加時間が表示されます


コマンド ( 通話データの表示 )
- total
通話の参加時間の合計を上位10名まで表示します

オプション
テキストチャンネルに投稿する : テキストチャンネルに表示結果を送信するかどうかを決めます、デフォルトはfalse(送信しない)になっています
- month
指定した月の通話の参加時間の合計を上位10名まで表示します

オプション
年 : 年を指定できます、デフォルトはコマンド時の年になります
月 : 月を指定できます、デフォルトはコマンド時の月になります
テキストチャンネルに投稿する : テキストチャンネルに表示結果を送信するかどうかを決めます、デフォルトはfalse(送信しない)になっています
- combination
コマンドを入力したユーザーとサーバー内での他のユーザーとの共通通話時間を上位10名まで表示します

オプション
テキストチャンネルに投稿する : テキストチャンネルに表示結果を送信するかどうかを決めます、デフォルトはfalse(送信しない)になっています
コマンド ( 設定 )
- set
コマンドを実行したテキストチャンネルを通話の開始/終了通知先のテキストチャンネルとして設定します

- notificationmode
テキストチャンネルへの通話の開始/終了通知を行うかどうかを設定します

- status
サーバー全体の通話情報と設定の確認ができます

Haskellで求根アルゴリズム
こんにちは、やきつか(@sy_t_)です。
最近はめっきり寒くなってきたのに、いつも半袖でいる知り合いがいて怖いです。
友人がHaskellで数値計算の記事を書いていて、全く同じ内容を書くのも面白いかな、といのうがこの記事の動機です。(友人の記事→Haskellで数値計算やってみた - Qiita)
はじめに
タイトルにある通り、今回は求根アルゴリズムの解説とHaskellによる実装を紹介したいと思います。
求根アルゴリズムとは、
二分法
アルゴリズム
二分法は、その名の通り区間を二分していくことで解を求める手法です。
具体的には、
実装
それでは、アルゴリズムに則って実装していきましょう。
ε :: Double ε = 1E-15 --0に限りなく近い正の定数 bisection :: (Double -> Double) --関数 -> Double --区間下限 -> Double --区間上限 -> Double --解 bisection f x1 x2 | abs (f x') < ε = x' -- -ε<f(x)<εならば中点を解として返す | f x1 * f x' > 0 = bisection f x' x2 --同符号ならばx1を中点と交換 | otherwise = bisection f x1 x' --それ以外ならばx2を中点と交換する where x' = (x1+x2)/2 --中点
実装終わり。解説していきます。
は、0とみなす値域を決定する定数で、0に近ければ近いほど解の精度が良くなります。
実際にその処理を実装しているのが次の行です。
abs (f x') < ε = x' -- -ε<f(x)<εならば中点を解として返す
さらにその次の行は、と同符号ならば
に置き換え自身に引数として渡し、
の場合も同様の処理をしています。(otherwiseとなっているのは、
と異符号ならば
と同符号なので)
| f x1 * f x' > 0 = bisectionMethod f x' x2 --同符号ならばx1を中点と交換 | otherwise = bisectionMethod f x1 x' --それ以外ならばx2を中点と交換する
ニュートン法
アルゴリズム
ニュートン法は、アイザック・ニュートンに由来する手法で、微分を用いて解を求める手法です。
この手法は次の漸化式によって、端的に表されます。

図で書くとこんな感じ。なぜ、上記のような漸化式になるかというと、
での接線の方程式が
つまり、
これを繰り返していくことにより、解に近づいていきます。
解の判定は二分法と同様に、εを用いて行います
実装
それでは、実装していきます。
ε :: Double ε = 1E-15 --0に限りなく近い正の定数 newton :: (Double -> Double) --関数 -> (Double -> Double) --導関数 -> Double --初期のx座標 -> Double --解 newton f f' x | abs (f x) < ε = x -- -ε<f(x)<εならば中点を返す | otherwise = newton f f' x' --次の点に進めて渡す where x' = x - f x / f' x --次のx座標
実装終わり。二分法との違いは、引数に導関数が増え、1つのx座標のみを引数にしているところですね。
ただ、この方法では導関数が明確な場合しか使えないので、適当に差分で置き換えて使うことが多いと思います。
ということで、微分を差分で置き換えて実装してみるとこんな感じ
ε :: Double ε = 1E-15 --0に限りなく近い正の定数 newton' :: (Double -> Double) --関数 -> Double --初期のx座標 -> Double --解 newton' f x | abs (f x) < ε = x -- -ε<f(x)<εならば中点を返す | otherwise = newton' f x' --次の点に進めて渡す where dx = 0.00001 --格子幅 f' x = ( f x - f (x-dx) ) / dx --微分ぽいもの x' = x - f x / f' x --次のx座標
オイラー法でローレンツアトラクタが見たい on Haskell
こんにちは! やきつか(@sy_t_)です。
最近やらなきゃいけないことが多いのですが、全然関係無いことをしてしまう自分に絶望してます。
はじめに
Haskellの勉強中に、「オイラー法の実装ならいい練習になるやん!」と思って実装しました。
プログラミングの一番の応用って数値計算だと思うんですよね(過激派)
オイラー法の実装だけでは面白くないので、適当な常微分方程式解いて終わります。
解析解のない微分方程式にはいろいろありますが、個人的に好きなローレンツ方程式にしました。
準備
それでは、対戦よろしくお願いします。
最近ハマっているパイプラインっぽい演算子を使わせて下さい。
(|>) :: (a -> b) -> (b -> c) -> (a -> c) f |> g = g.f
タプルを使いたくないので、時空座標を表すCoordinate型を作ってShowのinstanceにします。
data Coordinate = Crd {getT :: Double, getX :: Double, getY :: Double, getZ :: Double} instance Show Coordinate where show (Crd t x y z) = map show |> foldl1 (\s0 s1 -> s0 ++ "," ++ s1) $ [t, x, y, z]
ローレンツ方程式もついでに定義しておきます。
lorenz :: Coordinate -> Coordinate lorenz (Crd t x y z) = Crd t x' y' z' where x' = (-p)*x + p*y y' = (-x)*z + r*x - y z' = x*y - b*z p = 10 r = 28 b = 8/3
この段階で

こんな感じのことができます。
オイラー法を実装する
準備がととのったのでオイラー法を実装します。
eulerMethod :: Double -> Double -> (Coordinate -> Coordinate) -> Maybe Coordinate -> Maybe Coordinate eulerMethod _ _ _ Nothing = Nothing eulerMethod h tmax f (Just vector@(Crd t x y z)) | t < tmax = Just vector' | otherwise = Nothing where vector' = Crd t' x' y' z' t' = t + h x' = x + h * getX (f vector) y' = y + h * getY (f vector) z' = z + h * getZ (f vector)
刻み幅h、数値解の見たい上限時間tmax
微分方程式がと表される時のf
前ステップでの座標vectorを引数にとります。
Maybe Coordinate -> Maybe Coordinate
となっているのはiterate関数を使いやすくしたかっただけです。
t < tmaxの時はオイラー法で次のステップの座標を計算してJustで包んで返します。
tmax以降の時間はいらないので、その時はNothingを返します。
全体をNumericalCalcモジュールとします。
module NumericalCalc where f |> g = g.f data Coordinate = Crd {getT :: Double, getX :: Double, getY :: Double, getZ :: Double} instance Show Coordinate where show (Crd t x y z) = map show |> foldl1 (\s0 s1 -> s0 ++ "," ++ s1) $ [t, x, y, z] eulerMethod :: Double -> Double -> (Coordinate -> Coordinate) -> Maybe Coordinate -> Maybe Coordinate eulerMethod _ _ _ Nothing = Nothing eulerMethod h tmax f (Just vector@(Crd t x y z)) | t < tmax = Just vector' | otherwise = Nothing where vector' = Crd t' x' y' z' t' = t + h x' = x + h * getX (f vector) y' = y + h * getY (f vector) z' = z + h * getZ (f vector) lorenz :: Coordinate -> Coordinate lorenz (Crd t x y z) = Crd t x' y' z' where x' = (-p)*x + p*y y' = (-x)*z + r*x - y z' = x*y - b*z p = 10 r = 28 b = 8/3
ローレンツアトラクタを見る
全てが整ったので、Main.hsを実装します。先に全体を記載します。
import NumericalCalc h = 0.01 tmax = 10000 initialCoordinates = Crd 0 1 1 1 main = do let trace = iterate (eulerMethod h tmax lorenz) (Just initialCoordinates) let n = 10000 let path = "result.dat" writeFile path "" sequentiallyWrite path (take n trace) sequentiallyWrite filePath [] = return () sequentiallyWrite filePath (Nothing:xs) = return () sequentiallyWrite filePath ((Just x):xs) = appendFile filePath (show x ++ "\n") >> sequentiallyWrite filePath xs
import NumericalCalc
で先程作ったモジュールを使えるようにします。
h = 0.01 tmax = 10000 initialCoordinates = Crd 0 1 1 1
は刻み幅と上限と初期条件です。
sequentiallyWrite関数はファイルパスとMaybeなリストを引数に、失敗(Nothing)するか終端にたどり着くまでひたすらファイルに印字する関数です。(同機能のものが既にありそうな気がする、誰か教えて下さい)
main部はオイラー法の反復合成リストtraceとステップ数n、パスを宣言してsequentiallyWrite関数に渡してます。
Main.hsを実行して、これによって得られたresult.datをgnuplotで適当に表示します。

実行結果



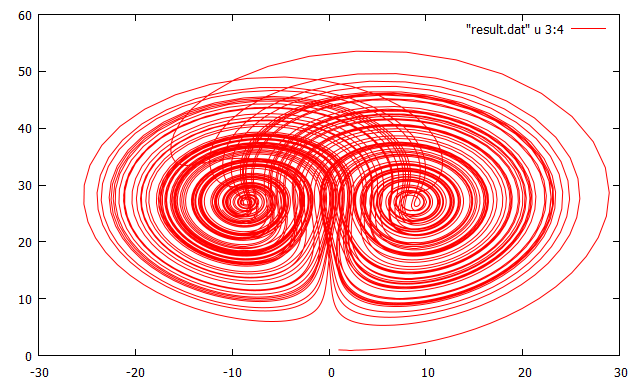
綺麗だ!!
Haskellで自然数から整数を構成する
こんにちは、やきつか(@sy_t_)です。
最近はとても暑いですね。僕は研究室の冷房強くしすぎてよくお腹を壊してるんですけど。
目次
はじめに
さて、今回は、純粋関数型言語であるHaskellを使って自然数を実装して、その自然数から整数を構成する、ということをやります。いきなりコードを貼り付けるのもアレなんで、自然数と整数の簡単な説明を通してから実装していきます。「それぐらいわかるわボケ」って人はその単元は飛ばしてください。
自然数ってなんぞや (ペアノの公理)
自然数ってなんでしょうかね。人に説明する時は「1,2,3,...って続く数字のことだよ」とか「0以上の全ての整数だよ」とかって言うんですかね。僕もそう言うと思います、めんどくさいし。
しかし、数学は厳密な学問なので、しっかりした定義が欲しくなります。そこで、ペアノさんが、次のような性質(ペアノの公理)を満たすものを自然数と呼ぶことにしようと決めました。自然数全体の集合をℕと表すことにします。
]
sucは後者関数と呼ばれる単射な写像で、"1を足す"ことに相当します。
ℕを外延的記法で書けば、という感じになります。
ここで、次のように各要素に名前をつけていきます。
このようにすると、我々がよくみるになりますね!
Haskellで自然数を実装する
自然数の定義はある程度理解できた(とする)ので、Haskellで自然数を実装してみましょう!
Haskellで自然数を定義するには、次のように書けばいいです。
data N = Zero | Suc N deriving (Eq, Ord, Show)
この文は、=の左辺と右辺に分けて読みます。dataは代数的データ型とよばれる、列挙型・構造体・共用体のようなものを生成するキーワードです、Cのstructのような使い方ですね。
=は代入だと思う人もいそうですが、「=の左辺っていうのは=の右辺に書いてあるもののことやで」の意味です。
右辺にあるZeroはコンストラクタとか構築子と呼ばれるやつで、列挙型の要素に相当します。
次にある|の記号は、「もしくは」と読みます。Suc NのSucは構築子なのですが、Nはフィールドとよばれるもので、なんらかの値(ここではN自身)にSucを適用したものです。
全体としては、「代数的データ型Nは、Zeroもしくは自身にSucを適用したもののことを言うんだな、うんうん」ぐらいの感じです。
代数的データ型に関しては、Haskell データ型・型クラス・型族 | Netsphere Laboratoriesあたりを読むといいと思います。
つまり、NというのはZeroもしくはSuc ZeroもしくはSuc (Suc Zero)もしくは...と無限の値を持つ代数的データ型です。
これは、Zeroを0、Sucを後者関数だとすると自然数そのものだと考えることができます。
「derivingってなんや?Eq,Ord,Show?」となっている人がいると思います、これは「代数的データ型Nの値は値同士で同値(Eq)であることを確かめられるし、比較(Ord)することもできるし、画面上に表示(Show)することができるんやで!!」というぐらいの意味です。詳しくは型クラス - ウォークスルー Haskellあたりを読んで下さい。(言い訳: Haskellの文法を解説する目的ではないので...)
自然数に二項演算を用意する
さて、Haskellで自然数を実装することができたので、足し算とか掛け算のような二項演算を作りましょう。
足し算は次のように定義します。
(+.) :: N -> N -> N Zero +. n = n n +. Zero = n n +. Suc m = Suc (n +. m)
これは、ペアノさんによる再帰的な加法の定義をそのままHaskellで書き下ろしただけです、これでちゃんと動きます。詳しくは加法 - Wikipediaを参考に。
同じ感じで、掛け算も実装していきます!
(*.) :: N -> N -> N Zero *. _ = Zero _ *. Zero = Zero n *. Suc m = n +. (n *. m )
+とか*に.(ドット)が付いてるのはHaskellの標準関数として+と*が定義されてしまっているからです、許して。
自然数が正しく動作していることを確認
全体のソースコードとしてはこんな感じ。
--いい感じに自然数を定義する data N = Zero | Suc N deriving (Eq, Ord, Show) --足し算を定義 Zero +. n = n n +. Zero = n n +. Suc m = Suc (n +. m) --掛け算を定義 Zero *. _ = Zero _ *. Zero = Zero n *. Suc m = n +. (n *. m )
ghciの対話形式で実行します。
- 同値性・順序性の確認

- 足し算の確認

Suc (Suc (Suc Zero))は3, Suc (Suc Zero)は2にあたるので、
Suc (Suc (Suc (Suc (Suc Zero))))が5=3+2という結果に一致していますね。
- 掛け算の確認

3*3=9になっていることを確認してください。(疲れた)
整数ってなんぞや
Haskellで自然数は実装できたので、一旦話を戻して、整数を数学的にどうやって作るのか説明したいと思います。
まず、自然数全体の2つの直積
を考えます。このを次のような同値関係
で割ってあげます。これが整数です。
の要素としては、
や
、
などが考えられると思います。これらの要素としての集合を、商写像
を用いて、
と表します。
さらに、を
、
を
と置くと、僕たちのよく知る整数
を垣間見ることができます!(何故このようにできるかは足し算や掛け算の実装でわかると思います。)
Haskellで整数を実装する
整数については理解できた(はず)なので、Haskellで実装していきましょう。といっても、そのまま書くだけなんですけど。
整数の元は2つの自然数全体の直積でした、これをHaskellで表現するには次のように書きます。
data Z = Z N N
「えっ、これだけ?」と思うかもしれません、これだけです。
「代数的データ型ZはNとNの2つの値を持つんだよ~」ぐらいのテンションです。(なげやり)
流石にこれだけでは、整数とは言えないので同値関係を定めておきます。これは、次のようにかけばOKです。
instance Eq Z where (Z n m) == (Z n' m') = n +. m' == m +. n'
「2つの自然数n,mを持つ整数と、2つの自然数n',m'を持つ整数が等しいとは、n+m'=m+n'が成立することである。」と読みます。
このように、ZをEq型クラスのインスタンスとして実装することで、いとも簡単に同値関係で割ることができます。やっぱりHaskellってすげぇよ。
整数を表示する時に、一意的に表示できるようにZをShow型クラスのインスタンスにします。
instance Show Z where show (Z n m) = show $ f (Z n m) where f :: Z -> Int f (Z Zero Zero) = 0 f (Z Zero (Suc m')) = (-1) + f (Z Zero m') f (Z (Suc n') Zero) = 1 + f (Z n' Zero) f (Z (Suc n') (Suc m')) | n' >= m' = 1 + f (Z n' (Suc m')) | n' < m' = (-1) + f (Z (Suc n') m')
これによって、例えばZ (Suc Zero) (Zero)もZ (Suc (Suc Zero)) (Suc Zero)も両方とも1と表示されます。(負の数ももちろん表示できる。)
整数に二項演算を用意する
整数において、足し算+は次のように定義されます。
また、掛け算は次のように定義されます。
なぜこのように定義すればうまくいくかは、実装のあと確認します。
Haskellで、上記の定義をそのまま書いてやります。
(Z n m) +.. (Z n' m') = Z (n +. n') (m +. m') (Z n m) *.. (Z n' m') = Z ( (n *. n') +. (m *. m') ) ( (n *. m') +. (n' *. m) )
+や*に.(ドット)が2つ付いてるのは、標準関数と上で自然数に対する演算で定義しているからです。(Num型クラスのインスタンスとして実装すればよかったのですが、+と*以外別にいらなかったので、このようにしました。)
整数が正しく動作していることを確認
ソースコード全体はこんな感じになりました。
--いい感じに自然数を定義して、演算も準備しておく data N = Zero | Suc N deriving (Eq, Ord, Show) Zero +. n = n n +. Zero = n n +. Suc m = Suc (n +. m) Zero *. _ = Zero _ *. Zero = Zero n *. Suc m = n +. (n *. m ) --整数はN×Nを適当な同値関係で割って構成する data Z = Z N N instance Eq Z where (Z n m) == (Z n' m') = n +. m' == m +. n' instance Show Z where show (Z n m) = show $ f (Z n m) where f :: Z -> Int f (Z Zero Zero) = 0 f (Z Zero (Suc m')) = (-1) + f (Z Zero m') f (Z (Suc n') Zero) = 1 + f (Z n' Zero) f (Z (Suc n') (Suc m')) | n' >= m' = 1 + f (Z n' (Suc m')) | n' < m' = (-1) + f (Z (Suc n') m') (Z n m) +.. (Z n' m') = Z (n +. n') (m +. m') (Z n m) *.. (Z n' m') = Z ( (n *. n') +. (m *. m') ) ( (n *. m') +. (n' *. m) )
それでは、確認していきます。
- 同値性の確認

- 表示の一意性

- 足し算

2-3=-1や2+3=5がうまく計算できていますね。
- 掛け算

2*3=6が計算できています。すごい。
あっ(-1)*(-1)ってどうなるんだろう

ちゃんと1になってくれましたね、めでたしめでたし。
楽しいゲーム 「宝石環(Gem-Ring)」と(-1)×(-1)=1
こんにちは、やきつか(@sy_t_)です。
(-1)×(-1)=1を代数的構造を崩さずに(無価値なたとえ話にならないように)説明しようと考えてたところ、よくわからなくなったので、よくわからないまま記事にしました。暇な方はお付き合いください。
ゲームのルール
楽しいゲームを考えたので、一緒に遊んでみましょう!
ゲーム名は「宝石環(Gem-Ring)」というもので、不思議な宝石にまつわるゲームです。
このゲームには、特殊な性質を持つ3つのジェム(宝石)があって、次のようなものです。
- ユニットジェム みんなが欲しがる、とても価値があるジェム、
で表す。
- ゼロジェム だれにも見向きされない全く無価値なジェム,、
で表す。
- インバースジェム 持っているだけで、ユニットジェムの価値を打ち消してしまう大変よろしくないジェム、
で表す。
ジェムの価値に関する表記
宝石袋(上の3種のジェムがはいった袋)から、適当に2つをだしてきて、それらの合計価値を表す表記があります。
具体的には次のように書きます。
表記 : 宝石A✦宝石B
意味 : 宝石Aと宝石Bの価値の合計
ジェムの価値に関するルール
宝石袋から適当にジェムを引っ張ってきて、それぞれ宝石A、宝石B、宝石Cとしておきます。
この時、どのような宝石についても次のルールがあります!
宝石Aと宝石Bの価値の合計と、宝石Cとの価値の合計は、宝石Aの価値と、宝石Bの価値と宝石Cの価値の合計との、価値の合計は同じ
つまり、価値を計算する時に、どっちから計算してもイイよ、ということです。
上の表記を使えば次のように書くことができます!
宝石Aと宝石Bの価値の合計は、宝石Bと宝石Aの価値の合計は同じ
当たり前すぎて、意味不明かもしれませんね。要するに、どっちに書いても一緒ってことです。
次のように書けます。
ゼロジェムとの価値の合計は何も変化しない
ゼロジェムOは価値のない宝石でしたから、他の宝石との価値の合計を計算しても価値が増えないことはお分かりですね。
次のように書けます。(こっちの方がわかりやすいかも)
価値の合計をゼロジェムの価値に等しくするようなジェム
インバースジェムはユニットジェムの価値を打ち消してしまう恐ろしいジェムなので、価値の合計
を計算するとゼロジェムの価値になってしまいます。
ユニットジェムとインバースジェムに限らず、価値を打ち消すようなジェムが必ず存在します。
そのようなジェムを元のジェムのインバースといいます。
ひとつの例としてと
があるだけです。
一般に、次のように表記します。
ジェムの錬金に関する表記
このゲームでは、ジェム同士を錬金することができます!
具体的には次のように書きます。
表記:
意味: 宝石Aをベースとして宝石Bを錬金したものの価値
重要なこと
宝石Aをベースとして宝石Bを錬金したものと、宝石Bをベースに宝石Aを錬金したものの価値は異なります!
現実の合金でも、割合が違ったら全く別の金属になりますからね!
ユニットジェムとの錬金は価値を変化させない
ユニットジェムは価値のある宝石ですが、錬金に関してはあまり良い性質を持ちません。
どんな宝石を、ユニットジェムとどのように錬金しても価値は変わりません!
つまり、というルールです!
価値の合計と錬金に関する決め事
最後のルール! これは価値の合計と錬金の記法の間の重要な決め事です。
次のように書いてあるものは、それぞれに錬金したものの価値の合計を意味する
これによって、いちいち錬金をとって価値を合計するという記法が短縮できますね!
ルールのまとめ
宝石の価値の合計のルール
- (1)
- (2)
- (3)
- (4)
宝石の錬金のルール
- (5)
- (6)
- (7)
- (8)
このゲームの目的
あなたは今、インバースジェムを2つ持っています。
インバースジェムは持っているだけで損なので、錬金して全く別の宝石に変えてしてしまおうとあなたは企みます。
しかし、インバースジェム同士の錬金に関するルールはないので結果がどうなるかわかりません。()
天才であるあなたは、上の錬金や価値に関するルールを知っています。
上のルールをうまく用いてインバースジェム同士の錬金の価値()を見いだすというのが、このゲームの目的です。
ヒント: はどうなるかな?
攻略(ネタバレ注意!!)
それでは、ゲームを攻略していきましょう!
を求めたいわけですが、まだ情報が足りないのでいきなりは導けません。
そこで、次のような性質を導いておきたいと思います。
: ゼロジェムと錬金するとゼロジェムになってしまう
今、なんでもいい宝石をAとしておき、の価値をみいだしてみようと思います。
(3)のルールを用いるとO=O✦Oなので
さらに、(6)のルールで
つまり、
となり、両辺にを加えて価値を計算すると
(4)のルールで、
導けました! 逆側も同じ手順でできるので、暇な読者はやってみるといいと思いますよ!
この新しい性質を用いて攻略をさらに進めてみましょう。
先程の性質を用いると、であることがわかると思います。
ところで、(4)のルールからなので、
とできます。
ここで、(6)のルールを用いて
(8)のルールからなので、
となります。
ここで、両辺にUを加えて価値を計算してみましょう。
(3)と(4)のルールから、
が導けました。
これは、インバースジェムとインバースジェム同士を錬金するとユニットジェムの価値と等しくなるということを示しています。
おめでとうございます、あなたはこの計算結果に驚愕し、インバースジェムをユニットジェムに作り変え、豪遊して余生を過ごすのでした。おしまい。
まとめ
もともとあるルールをこねくり回してを導出できたわけですが、これは(-1)×(-1)=1を証明するステップと同じになっています(大半の人は分かっていると思う)。実は上に書いてるルールは環(Ring)という代数的構造が満たすもので、実数と実数の足し算・掛け算も同じルールを持っています。(-1)×(-1)=1のようなものは一例で、環のルールから他にも様々な"公式"を導出することができます。
正直、自分で見返してもよくわからないので、よくわからなかった方は他にもっとわかりやすい記事がたくさんあるので、そちらを参照してください。
MPS法とナビエ・ストークス方程式 概論
こんにちは、やきつか(@sy_t_)です。
大学に受かって暇なのでブログをはじめました(開設自体は1年前)。
せっかく研究で流体のシュミレーションをしているので最初はそれについて書いていくのも一興かなと。
とりあえずは、この記事を出発点として、MPS法の概要から具体的手法、シュミレーション結果まで何回かに分けて書いていこうと思います。
初学者なので、間違いがあったら教えてくれると幸いです。
MPS法って一体何なの? ナビエ・ストークス方程式?
早速ですが。
MPS法は、東京大学の越塚誠一さんという方が開発した手法で、Moving Particle Semi-implicitの頭文字をとったものになります。
MPS法を説明するためには、まず粒子法というものを説明しなければなりません。
Wikipediaを引いてみますと、
粒子法(りゅうしほう)とは、連続体に関する方程式を数値的に解くための離散化手法の一つで、計算対象物を粒子の集まりとして表すことからこのように呼ばれる。
主に流体解析,構造解析に用いられる手法で、代表的なものとしてDEM(Distinct Element Method)法, SPH(Smoothed Particle Hydrodynamics)法, MPS(Moving Particle Semi-implicit)法などがある。
と書いてあります。例のごとくwikipediaはお硬い文章なので、噛み砕いて説明しようと思います。
まず、"連続体"についてですが、弾性体と流体のことです。弾性体は力が加わっていなければ元の形に戻るような物体(ゴムボールとか)で、流体は流れる物体(気体・液体とか)のことですね。
この連続体である流体に関する挙動を記述するのが(あの)ナビエ・ストークス方程式です!
次に、そのナビエ・ストークス方程式を示します。
ぼくは物理屋さんではないので導出に至る経緯は知らないんですけど、ニュートンの運動方程式に比べて形がおぞましい。
上の方程式を扱えればいいんですけど、さすがにこのままでは複雑すぎるので、様々な条件を仮定することで簡単な形に持っていきます。
流体の粘性率が一定で、非圧縮性の流れであることを仮定すれば、次のような方程式へと変貌します。
まず、方程式の各文字について説明していきたいと思います。
まず最も重要なのはvですね。vは流体の速度場です、速度は3次元だと3つの成分を持つのでベクトルです。つまりvは速度のベクトル場になります。
ρは流体の密度場で、直感的には流体がある地点にどれぐらい密集しているかをあらわしています
。
p(ρと間違えてはいけない)は圧力場で、空間にどのように圧力が分布しているかを示しています。
νは粘性係数で、物体の粘性がどれぐらいなのかを示します、スカラーです。
gは外力です、重力などが相当します。
次に方程式の各項について見ていきたいと思います。
左辺の項は速度のラグランジュ微分になっていて、流れと同じ動きをする座標系からみた加速度になっています。
右辺の第一項は圧力勾配項と呼ばれるもので、空間の圧力の傾きが最小となるような方向を向く力を表しています、ベクトルになります。
右辺の第二項は粘性項と呼ばれるもので、流体の速度をまわりに近づけようとする力です。
右辺の第三項は外力で、重力下ならば(0,0,-9.8)のようなベクトルが常にかかることを意味します。
かなり、大雑把な説明になりましたがナビエ・ストークス方程式はこういうものです。
粒子法は、流体を粒子、つぶつぶの集まりとして考えて、そのつぶつぶがナビエ・ストークス方程式に従って動くように見せかける手法です。
お手元にあるコンピュータでこれを解くには、なんらかの"離散化"をしてあげる必要があって、その手法にDEM,SPH,MPSなどの種類があるイメージです。
次回以降は。MPS法でナビエ・ストークス方程式をどのように"離散化"するのか、具体的に書いていこうと思います!
